01
sur 05
Nombres babyloniens
Trois principaux domaines de différence par rapport à nos chiffres
Nombre de symboles utilisés dans les mathématiques babyloniennes
Imaginez combien il serait plus facile d'apprendre l'arithmétique dans les premières années si tout ce que vous aviez à faire était d'apprendre à écrire une ligne comme moi et un triangle. C'est essentiellement tout ce que les anciens de la Mésopotamie devaient faire, bien qu'ils les aient variés ici et là, en s'allongeant, en tournant, etc.
Ils n'avaient ni stylos ni crayons, ni papier d'ailleurs. Ce qu'ils ont écrit était un outil que l'on utiliserait en sculpture, car le médium était de l'argile. Que ce soit plus difficile ou plus facile à apprendre à manipuler qu'un crayon est un jeu d'enfant, mais jusqu'à présent, ils sont en avance dans le département de facilité, avec seulement deux symboles de base à apprendre.
Base 60
L'étape suivante jette une clé dans le département de simplicité. Nous utilisons un Base 10, un concept qui semble évident puisque nous avons 10 chiffres. Nous en avons en fait 20, mais supposons que nous portons des sandales avec des orteils de protection pour éviter le sable le désert, chaud du même soleil qui ferait cuire les tablettes d'argile et les conserverait pour que nous trouvions des millénaires plus tard. Les Babyloniens ont utilisé cette base 10, mais seulement en partie. En partie, ils ont utilisé la base 60, le même nombre que nous voyons tout autour de nous en minutes, secondes et degrés d'un triangle ou d'un cercle. Ils étaient des astronomes accomplis et leur nombre pouvait donc provenir de leurs observations du ciel. La base 60 contient également divers facteurs utiles qui facilitent le calcul avec. Pourtant, avoir à apprendre la Base 60 est intimidant.
Dans "Hommage à Babylonie" [La Gazette Mathématique, Vol. 76, n ° 475, "L'utilisation de l'histoire des mathématiques dans l'enseignement des mathématiques" (mars 1992), pp. 158-178], l'écrivain-enseignant Nick Mackinnon dit qu'il utilise les mathématiques babyloniennes pour enseigner aux enfants de 13 ans des bases autres que 10. Le système babylonien utilise la base 60, ce qui signifie qu'au lieu d'être décimal, il est sexagésimal.
Notation de position
Le système de nombres babylonien et le nôtre dépendent de la position pour donner de la valeur. Les deux systèmes le font différemment, en partie parce que leur système manquait d'un zéro. Apprendre le système de positionnement babylonien de gauche à droite (haut en bas) pour un premier goût d'arithmétique de base n'est probablement plus difficile que d'apprendre notre 2-directionnel, où nous devons nous rappeler l'ordre des nombres décimaux - en augmentant à partir de la décimale, les uns, les dizaines, les centaines, puis se déployant dans l'autre sens de l'autre côté, pas de colonne oneths, juste des dixièmes, des centièmes, millièmes, etc.
J'entrerai dans les positions du système babylonien sur d'autres pages, mais il y a d'abord quelques mots importants à apprendre.
Années babyloniennes
Nous parlons de périodes d'années en utilisant des quantités décimales. Nous avons une décennie pour 10 ans, un siècle pour 100 ans (10 décennies) ou 10X10 = 10 ans au carré, et un millénaire pour 1000 ans (10 siècles) ou 10X100 = 10 ans en cubes. Je ne connais pas de terme plus élevé que cela, mais ce ne sont pas les unités utilisées par les Babyloniens. Nick Mackinnon fait référence à une tablette de Senkareh (Larsa) de Sir Henry Rawlinson (1810-1895) * pour les unités utilisées par les Babyloniens et pas seulement pour les années concernées, mais aussi pour les quantités impliquées:
- soss
- ner
- sar.
sossnersosssarsoss
Toujours pas de bris d'égalité: il n'est pas nécessairement plus facile d'apprendre les termes de l'année quadratique et cubique dérivés du latin que ce sont des mots babyloniens d'une syllabe qui n'impliquent pas le cubage, mais la multiplication par 10.
Qu'est-ce que tu penses? Aurait-il été plus difficile d'apprendre les bases du nombre en tant qu'écolier babylonien ou en tant qu'élève moderne dans une école anglophone?
* George Rawlinson (1812-1902), le frère d'Henry, montre un tableau de carrés transcrit simplifié dans Les sept grandes monarchies de l'ancien monde oriental. Le tableau semble être astronomique, basé sur les catégories d'années babyloniennes.
Toutes les photos proviennent de cette version numérisée en ligne d'une édition du 19e siècle de George Rawlinson's Les sept grandes monarchies de l'ancien monde oriental.02
sur 05
Les nombres de mathématiques babyloniennes
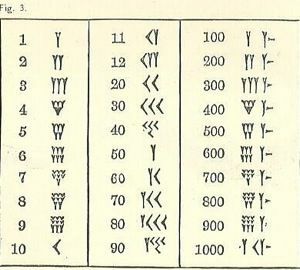
Depuis que nous avons grandi avec un système différent, les chiffres babyloniens prêtent à confusion.
Au moins, les chiffres vont de haut à gauche à bas à droite, comme notre système arabe, mais le reste semblera probablement inconnu. Le symbole pour un est une forme de coin ou en forme de Y. Malheureusement, le Y représente également un 50. Il existe quelques symboles distincts (tous basés sur le coin et la ligne), mais tous les autres nombres sont formés à partir d'eux.
N'oubliez pas que la forme d'écriture est cunéiforme ou en forme de coin. En raison de l'outil utilisé pour dessiner les lignes, la variété est limitée. Le coin peut ou non avoir une queue, dessinée en tirant le stylet d'écriture cunéiforme le long de l'argile après avoir imprimé la forme triangulaire partielle.
Le 10, décrit comme une pointe de flèche, ressemble un peu à
Trois rangées de jusqu'à 3 petits 1 (écrits comme des Y avec des queues raccourcies) ou 10 (un 10 est écrit comme
03
sur 05
1 ligne, 2 lignes et 3 lignes

Il existe trois ensembles de nombres cunéiformes clusters mis en évidence dans l'illustration ci-dessus.
Pour l'instant, nous ne nous soucions pas de leur valeur, mais de montrer comment vous verriez (ou écririez) de 4 à 9 du même nombre regroupés. Trois vont de suite. S'il y a un quatrième, cinquième ou sixième, il va en dessous. S'il y a un septième, huitième ou neuvième, vous avez besoin d'une troisième ligne.
Les pages suivantes contiennent des instructions pour effectuer des calculs avec le cunéiforme babylonien.
04
sur 05
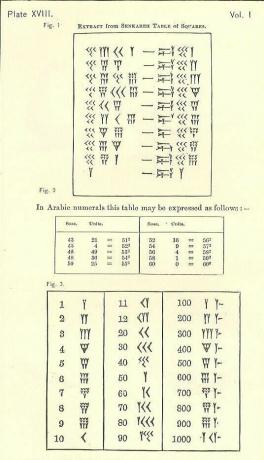
La table des carrés
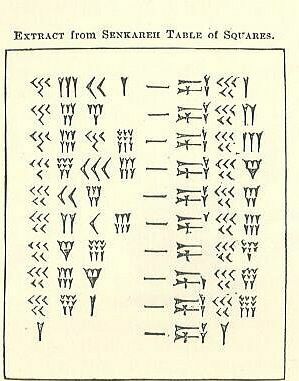
D'après ce que vous avez lu ci-dessus sur le soss - dont vous vous souviendrez est le Babylonien depuis 60 ans, le coin et la pointe de flèche - qui sont des noms descriptifs pour les marques cunéiformes, voyez si vous pouvez comprendre comment ces calculs fonctionnent. Un côté de la marque en forme de tiret est le nombre et l'autre est le carré. Essayez-le en groupe. Si vous ne pouvez pas le comprendre, regardez l'étape suivante.
05
sur 05
Comment décoder la table des carrés

Pouvez-vous le comprendre maintenant? Donnez-lui une chance.
...
Il y a 4 colonnes claires sur le côté gauche suivies d'un signe en forme de tiret et 3 colonnes sur la droite. En regardant à gauche, l'équivalent de la colonne 1 est en fait les 2 colonnes les plus proches du "tiret" (colonnes intérieures). Les 2 autres colonnes extérieures sont comptées comme la colonne des années 60.
- Le 4-
- Les 3-Y = 3.
- 40+3=43.
- Le seul problème ici est qu'il y a un autre numéro après eux. Cela signifie qu'ils ne sont pas des unités (la place des uns). Le 43 n'est pas un 43, mais un 43-60, car c'est le système sexagésimal (base 60) et il est dans le soss comme l'indique le tableau inférieur.
- Multipliez 43 par 60 pour obtenir 2580.
- Ajoutez le numéro suivant (2-
- Vous en avez maintenant 2601.
- C'est le carré de 51.
La ligne suivante a 45 dans le soss, donc vous multipliez 45 par 60 (ou 2700), puis ajoutez le 4 de la colonne des unités, vous avez donc 2704. La racine carrée de 2704 est 52.
Pouvez-vous comprendre pourquoi le dernier nombre = 3600 (60 au carré)? Astuce: pourquoi n'est-ce pas 3000?