Feuilles de travail pré-algèbre pour l'écriture d'expressions

sur 05

Feuille de calcul des expressions algébriques 1

Écrivez l'équation ou l'expression algébriquement.

Imprimez la feuille de calcul PDF ci-dessus, les réponses sont sur la deuxième page.

Une expression algébrique est une expression mathématique qui aura des variables, des nombres et des opérations. La variable représentera le nombre dans une expression ou une équation. Les réponses peuvent varier légèrement. Être capable d'écrire des expressions ou des équations algébriquement est un concept de pré-algèbre qui est nécessaire avant de prendre algèbre.

Les connaissances préalables suivantes sont requises avant de faire ces feuilles de travail:

Comprendre qu'une variable est une lettre telle que x, y ou n et qu'elle représentera le nombre inconnu.

Qu'une expression est une déclaration en mathématiques qui ne contiendra pas de signe égal mais qui peut contenir des nombres, des variables et des signes d'opération tels que +, - x etc. Par exemple, 3y est une expression.

instagram viewer

Qu'une équation est une déclaration en mathématiques qui contient un signe égal.

Il devrait y avoir une certaine familiarité avec entiers qui sont des nombres entiers ou des nombres entiers avec un signe négatif.

Il est également important de comprendre et de connaître les termes: quotient, produit, somme, augmenté et diminué en ce qui concerne les opérations. Par exemple, lorsque le mot somme est utilisé, vous devrez savoir que l'opération implique l'ajout ou l'utilisation du signe +. Lorsque le mot quotient est utilisé, il fait référence au signe de division et lorsque le mot produit est utilisé, il fait référence au signe de multiplication qui est indiqué par a. ou en mettant la variable à côté du nombre comme dans 4n ce qui signifie 4 x n

sur 05

Feuille de calcul de l'expression algébrique 2

Feuilles de travail sur l'expression algébrique # 2 — Feuille de calcul de l'expression algébrique 2 sur 5.RÉ. Russell

Écrivez l'équation ou l'expression algébriquement.

Imprimez la feuille de calcul PDF ci-dessus, les réponses sont sur la deuxième page.

Écrire les expressions ou les équations algébriques et se familiariser avec le processus est une compétence clé requise avant de simplifier les équations algébriques. Il est important d'utiliser le. lorsque vous faites référence à la multiplication car vous ne voulez pas confondre la multiplication avec x la variable. Bien que les réponses soient fournies sur la deuxième page de la feuille de calcul PDF, elles peuvent varier légèrement en fonction de la lettre utilisée pour représenter l'inconnu. Lorsque vous voyez des déclarations comme:
Un nombre multiplié par cinq équivaut à cent vingt, au lieu d'écrire n x 5 = 120, vous écririez 5n = 120, 5n signifie multiplier un nombre par 5.

sur 05

Feuille de calcul de l'expression algébrique 3

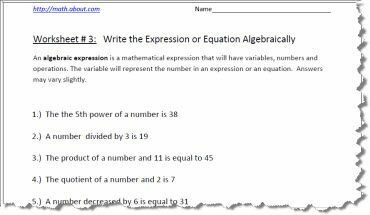
Feuille de travail sur l'expression algébrique n ° 3.RÉ. Russell

Écrivez l'équation ou l'expression algébriquement.

Imprimez la feuille de calcul PDF ci-dessus, les réponses sont sur la deuxième page.

Des expressions algébriques sont requises dans le programme dès la 7e année, cependant, les bases de l'exécution du tas se produisent en 6e année. La pensée algébrique se produit en utilisant le langage de l'inconnu et en représentant l'inconnu avec une lettre. Lorsque vous présentez une question comme: La différence entre un nombre et 25 est 42. La différence devrait signifier que la soustraction est implicite et sachant que, l'énoncé ressemblerait alors à: n - 24 = 42. Avec la pratique, c'est devenu une seconde nature!

J'ai eu un enseignant qui m'a dit une fois, rappelez-vous la règle du 7 et revisitez. Il pensait que si vous exécutiez sept feuilles de calcul et revisitiez le concept, vous pourriez prétendre que vous seriez sur le point de comprendre. Jusqu'à présent, cela semble avoir fonctionné.